Introduksjon
Vi vil nå jobbe videre med skilpaddekunsten fra tidligere. Denne gangen skal vi tegne forskjellige figurer som kalles fraktaler. Fraktaler er figurer som bygges opp av små kopier av seg selv. I løpet av leksjonen vil vi også jobbe mer med funksjoner og rekursjon.

Steg 1: Husker du skilpadden?
Vi har brukt skilpaddebiblioteket turtle tidligere. Du husker
kanskje kode som lignet på den under?
from turtle import *
shape('turtle')
shapesize(2)
bgcolor('darkblue')
color('yellow')
speed(3)
forward(270)
Sjekkliste
-
Skriv inn programmet over. Lagre det med navnet
snoflak.pyog kjør det. En rett strek skal tegnes på skjermen. -
Endre litt på tallene og fargene i koden slik at du husker hva de forskjellige kommandoene gjør. Finner du en fargekombinasjon du liker?
Steg 2: En fraktal
En fraktal er en figur som er bygd opp av mindre kopier av seg selv. Vi skal nå se på hvordan vi kan tegne denne figuren:
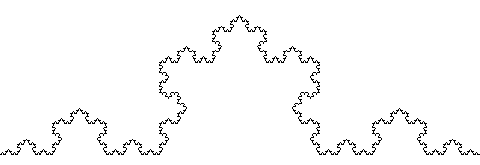
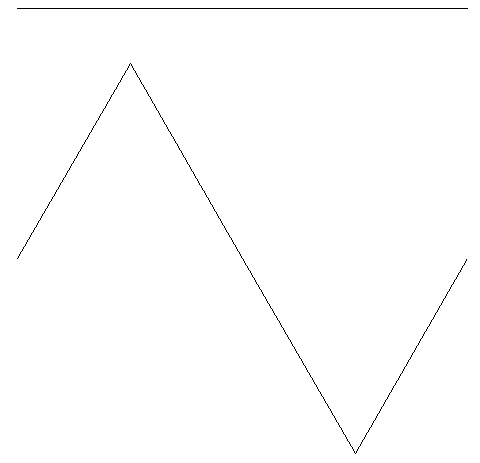
Dette er en fraktal, klarer du å se at den består av mange små kopier av seg selv? Det er kanskje lettere å se i de neste figurene?
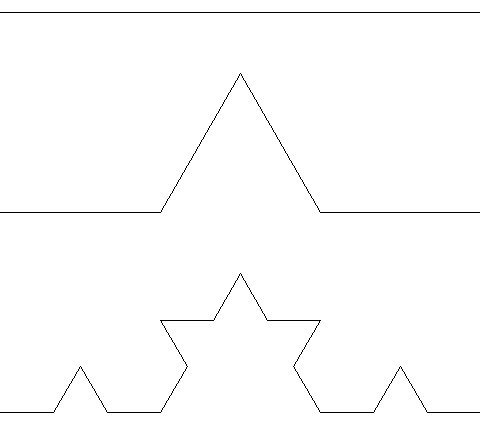
Den øverste figuren er bare en rett strek. Den neste figuren består av fire rette streker som danner et enkelt fjell. Hvis du nå ser nærmere på den tredje figuren ser du at den består av fire kopier av det enkle fjellet, igjen lagt slik at de danner et litt mer komplisert fjell.
Hvis du nå ser tilbake på den første figuren, ser du hvordan den består av mange små kopier av slike fjell?
Steg 3: Vi tar det stegvis
Vi skal se på hvordan vi kan lage funksjoner som kan tegne figurene over.
Sjekkliste
-
Den rette streken har vi jo allerede tegnet. La oss bare endre litt i programmet vårt slik at dette blir en funksjon:
from turtle import * shape('turtle') shapesize(2) bgcolor('darkblue') color('yellow') speed(3) def en(): forward(270) en()Husk at vi må kalle funksjonen for at den skal bli gjort.
-
La oss nå legge til en funksjon
to()som tegner den andre figuren, det enkle fjellet. Skriv denne funksjonen i den samme filen.def to(): forward(90) left(60) forward(90) right(120) forward(90) left(60) forward(90) to()Ser du sammenhengen mellom figuren og koden?
-
Kjør programmet ditt. Husk at du kan styre hvilke figurer som tegnes med hvilke funksjoner du kaller. Selv om både
enogtoer definert trenger du ikke kalle begge funksjonene. -
I
tohar vi bruktforward(90), mens ienbrukte viforward(270). Det betyr at vi har tegnet den rette streken tre ganger mindre. Men vi har brukt vinkler slik at de fire strekene itotilsammen blir like lang som den ene streken ien.La oss endre litt i funksjonene slik at vi bruker
eni stedet forforwardnår vi definererto.def en(lengde): forward(lengde) def to(lengde): en(lengde / 3) left(60) en(lengde / 3) right(120) en(lengde / 3) left(60) en(lengde / 3) to(270) -
Kjør programmet igjen. Tegnes fortsatt de samme figurene?
-
Vi vil nå tegne den tredje figuren. En måte å gjøre dette på kan være å kombinere
forward,leftogrightslik vi opprinnelig gjorde forto. Du trenger ikke skrive inn denne koden, men se på den og sammenlign med figuren. Ser du at det stemmer?def tre(): forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) left(60) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) left(60) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) -
Dette er en kjedelig måte å programmere på: Vi må skrive kjempemye kode, det er veldig lett å gjøre feil og det tar tid å gjøre endringer i koden.
Hvis du ser litt nærmere på koden vil du se at linjene
forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30)går igjen flere ganger. Sammenlign disse linjene med funksjonen
tofra tidligere. Ser du en måte vi kan forenkle koden vår? -
Vi har sett at koden til
trebestår av flere kopier av koden tilto, bare krympet. Da kan vi jo gjøre samme trikset som tidligere, vi bare kallerto. Skriv inn følgende kode i den samme filen somenogto:def tre(lengde): to(lengde / 3) left(60) to(lengde / 3) right(120) to(lengde / 3) left(60) to(lengde / 3) tre() -
Klarer du å tegne alle tre figurene nå?
Steg 4: Her kan vi kombinere
Nå skal vi lage en funksjon som kan tegne alle tre figurene!
Sjekkliste
Nå kommer det morsomste. Før vi kaster bort tid på å lage flere
funksjoner fire, fem og kanskje seks, skal vi se at vi kan lage
en funksjon som kan lage alle disse for oss!
- Sammenlign funksjonene
toogtre. Ser du at de er nesten helt like?
Vi skal nå bruke noe som kalles rekursjon for å lage en funksjon som
gjør jobben til både en, to og tre. Rekursjon husker du kanskje
fra tidligere. Det betyr at vi lager en funksjon som kaller seg selv,
men for å gjøre noe som er litt enklere.
Med rekursjon ser man gjerne på det enkle tilfellet og det generelle
tilfellet. For disse figurene er en det enkle tilfellet hvor vi bare
trenger å tegne en rett strek.
-
Legg til denne funksjonen. Dette er det enkle tilfellet:
def fjell(lengde, dybde): if dybde == 1: forward(lengde) returnHer bruker vi
returnfor å si at vi ikke vil gjøre mer for det enkle tilfellet. -
Det generelle tilfellet er det vi har sett tidligere i
toogtre. Med den nye variabelendybdekan vi lage bådetoogtremed samme kode. Utvid funksjonenfjellslik at den ser slik ut:def fjell(lengde, dybde): if dybde == 1: forward(lengde) return fjell(lengde / 3, dybde - 1) left(60) fjell(lengde / 3, dybde - 1) right(120) fjell(lengde / 3, dybde - 1) left(60) fjell(lengde / 3, dybde - 1)Kjenner du igjen koden fra tidligere?
-
Prøv å tegn
fjell(270, 2)og
fjell(270, 3)Gir dette samme resultat som
to(270)ogtre(270)? -
Den nye funksjonen gjør enda mer enn
toogtre. Vi kan bruke enda større dybde. Prøv for eksempelfjell(270, 6). Denne vil bruke litt tid. Brukspeed(11)for at skilpadden skal bevege seg så raskt som mulig.
Steg 5: Et snøflak
Vi skal nå kombinere flere slike fjell til et fint snøflak.
Sjekkliste
-
Til sist skal vi kombinere flere kall til
fjell-funksjonen vår for å tegne det fine snøflaket du så helt først i oppgaven. Ser du hvordan snøflaket består av tre fjell?Legg til denne funksjonen:
def snoflak(lengde, dybde): for i in range(3): fjell(lengde, dybde) right(120) -
Prøv å kall denne
snoflak-funksjonen med forskjellige lengder og dybder.
Dette snøflaket er en av de mest kjente fraktalene. Det har fått navnet Kochs snøflak fordi en av de første som studerte denne figuren het Helge von Koch.
Steg 6: Firkantede fjell
La oss se på en variant av snøflaket.
Sjekkliste
Vi vil nå lage en fraktal på samme måte som Koch-figuren men med en litt form. I stedet for en trekant som danner fjellet vil vi bruke en firkant som i figuren under:
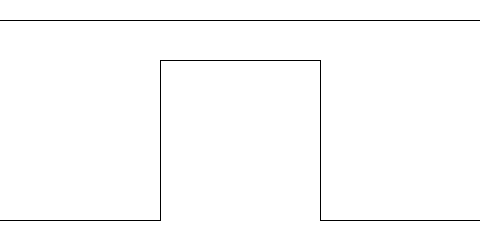
-
Lag en ny fil som du kaller
firkantfjell.py. -
Som tidligere så kan vi prøve å tegne dette nye fjellet med funksjoner for hvert steg. For eksempel
from turtle import * shape('turtle') shapesize(2) bgcolor('darkblue') color('yellow') speed(3) def en(lengde): forward(lengde) def to(lengde): en(lengde / 3) left(90) en(lengde / 3) right(90) en(lengde / 3) right(90) en(lengde / 3) left(90) en(lengde / 3) to(270) -
Men vi har jo lært at det er mye bedre å bruke rekursjon. Vi vil lage en funksjon som kan tegne mange forskjellige firkantfjell ved at den kaller seg selv.
Prøv selv om du kan skrive denne. Se på hvordan vi laget
fjelltidligere, og på hvordan vi lagetenogtonå sist.def firkantfjell(lengde, dybde): if dybde == 1: # Her må du programmere det enkle tilfellet return # Her må du programmere det generelle tilfellet -
Test koden din. Blir det riktig? Nedenfor ser du et eksempel hvor vi har laget et firkantfjell med dybde 6.
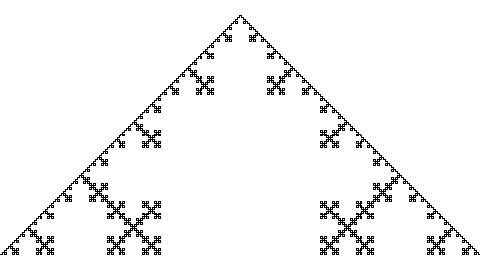
Steg 7: Trekanter
Vi trenger ikke bare bruke rette streker for det enkle tilfellet.
Sjekkliste
Vi skal nå lage en fraktal basert på trekanter. La oss se på de første stegene:
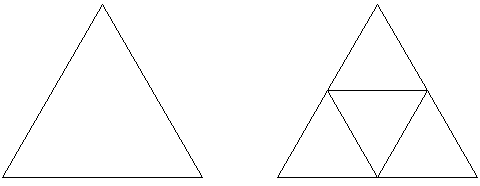
Her ser vi at vi har en trekant som byttes ut med tre mindre trekanter.
-
Lag en ny fil
trekant.pyog legg til de vanlige kommandoene på toppen av filen. -
I det enkle tilfellet vil vi nå tegne en trekant. Det kan vi gjøre på denne måten:
def trekant(lengde, dybde): if dybde <= 1: pendown() for i in range(3): forward(lengde) left(120) penup() return -
For det generelle tilfellet må vi stable tre trekanter. Det kan vi gjøre for eksempel med koden under. Sammenlign koden med figuren. Ser du sammenhengen?
trekant(lengde / 2, dybde - 1) forward(lengde / 2) trekant(lengde / 2, dybde - 1) left(120) forward(lengde / 2) right(120) trekant(lengde / 2, dybde - 1) right(120) forward(lengde / 2) left(120) -
Tegn noen trekanter med forskjellig dybde og størrelse. Denne fraktalen er også ganske kjent, og går ofte under navnet Sierpinski-trekanten.
Prøv selv
Det finnes mange fraktaler, og du kan lage dine helt egne også!
Prøv for eksempel å endre litt på vinklene og lengdene i fjell- eller
firkantfjell-funksjonene.
Eller kanskje du kan lage en helt annen figur? Prøv og tegn dine egne
en- og to-figurer som du så oversetter til Python.
Her er et forslag til en figur du kan prøve, men prøv også å lage dine egne!