Introduksjon
Nå som du kan tegne mangekanter (hvis du ikke har gjort leksjonen om mangekanter, bør du gjøre dem først), skal vi se på en litt spesiell type mangekanter: de regulære mangekantene. Det vil si de mangekantene hvor lengden av hver kant er lik og vinkelen i hvert hjørne er lik. Vi skal også tegne deres nære slektninger, de regulære stjernene.
Det er en stor fordel å kunne litt trigonometri før man slår seg løs på disse oppgavene, men vi skal prøve å gi korte forklaringer av de konseptene som brukes i leksjonen.
Sinus og cosinus
Før vi begynner å tegne regulære mangekanter, skal vi bare ta en titt på to trigonometriske funksjoner som vi kommer til å bruke mye: sinus og cosinus. Vi skal se på dem spesifikt i forbindelse med sirkler.
- Ethvert punkt langs omrisset av sirkelen befinner seg like langt fra
midten av sirkelen. Denne avstanden er radius i sirkelen, som regel
skriver vi bare
ri figurer og formler.
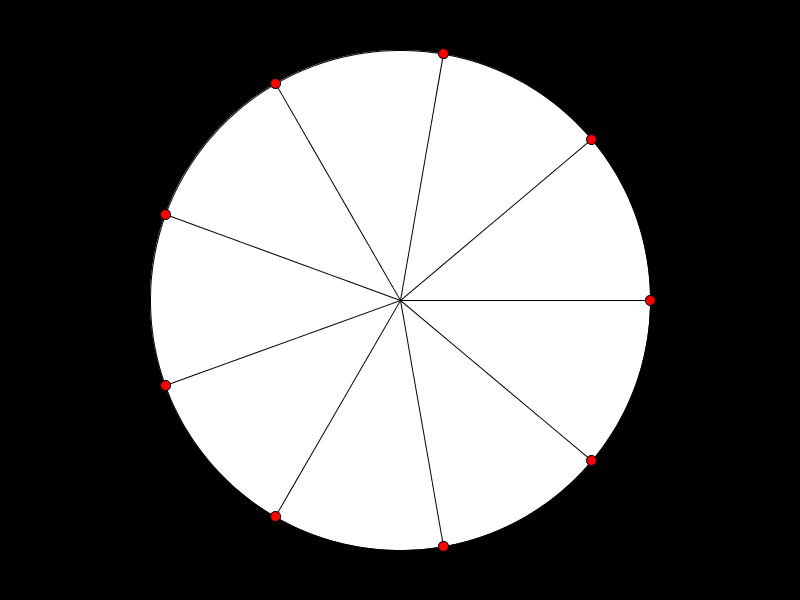
- Vi kan tegne en rettvinklet trekant som ligger vannrett og strekker seg fra midten av sirkelen til ett av disse punktene.
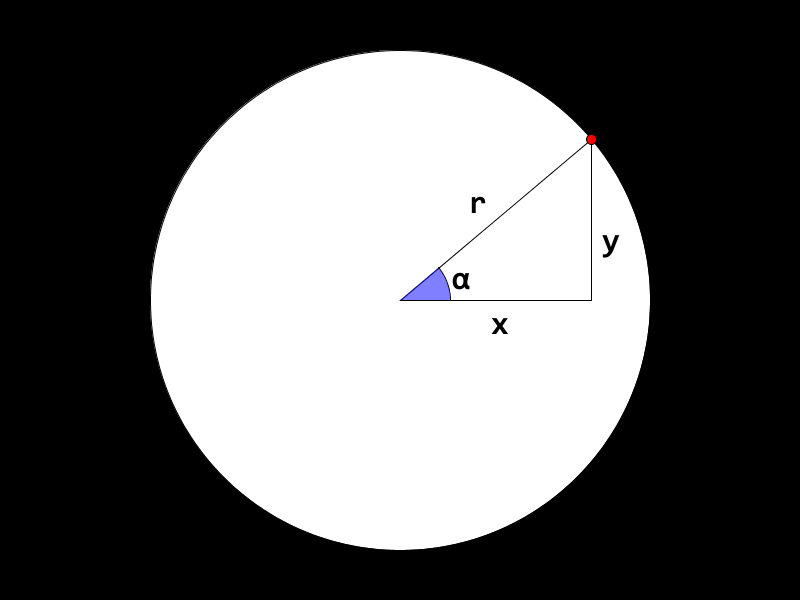
-
Hvis vi sier at sentrum av sirkelen ligger i punktet (0, 0), altså X og Y er null i midten av sirkelen, kan vi enkelt regne ut X og Y for punktet i omrisset. To av sidene i trekanten ovenfor viser da X og Y. Den siste siden er linjen fra sentrum med lengde
r. Derfor har vi kalt sidenex,yogr; navnet kan brukes for lengdene til sidene også. For vinkler er det vanlig å bruke greske bokstaver, og vi har her bruktα, alfa. -
Lengden på sidene
xogyer gitt av funksjonene sinus og cosinus, vinkelenαogr, altså radien til sirkelen. De korte sidene som sammen lager det rettvinklede hjørnet, kalles kateter og den lange siden med lengderkalles hypotenus. Lengden på kateten som er med på hjørnet med vinkelenα, har lengdencos(α) * r. Denne kateten kalles gjerne den hosliggende kateten, og mange bruker huskeregelen: Hos blir cos, for å huske hvilken av de to sidene som bruker cosinus og sinus. Lengden på den andre kateten, kalt den motstående kateten ersin(α) * r.
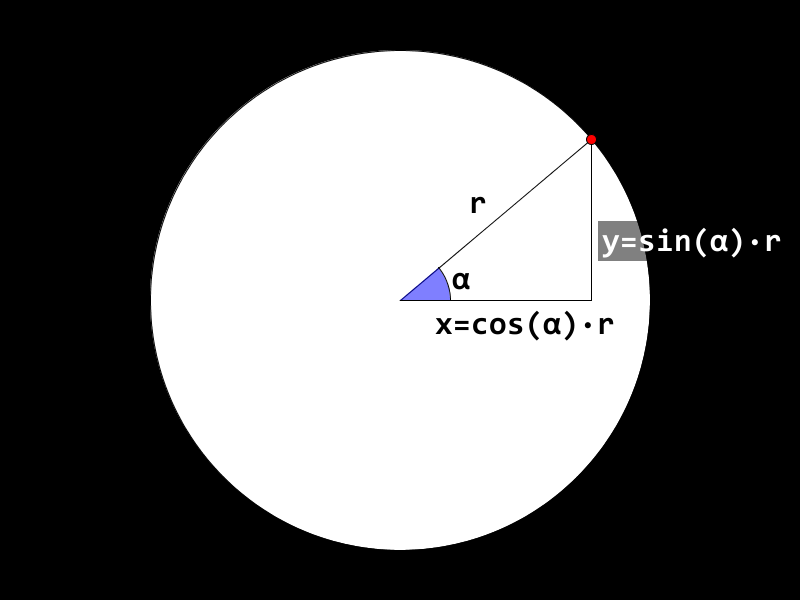
- Det virker kanskje litt merkelig når du bare får formlene sånn, men
sinus og cosinus er definert som forholdene mellom hypotenusen,
r, og katetene,xogy.sin(α) = y / rogcos(α) = x / r. Vi skal ikke se på hvordan man finner disse tallene ut fra vinkelen, men det skal vi la datamaskinen gjøre for oss.
Regulære mangekanter
La oss tegne opp noen regulære mangekanter. Det vil si mangekanter der avstanden mellom hvert hjørne er lik, altså de er likesidede, og vinkelen i hvert hjørne er lik, altså de er likevinklede. Da lurer du kanskje på hvordan du skal få til dette. Hjørnene i en regulær mangekant fordeler seg jevnt langs omrisset av en sirkel. Derfor kan vi bruke formlene for katetene for å regne ut hvor hjørnene skal være. Opptegningen ellers er som for vanlige mangekanter.
-
Vi begynner med å tegne opp en regulær pentagon (femkant).
int KANTER = 5; float vinkel = 360.0 / KANTER; void setup() { size(600, 600); } void draw() { background(0); beginShape(); for (int hjorne = 0; hjorne < KANTER; hjorne++) { vertex(300 + cos(radians(vinkel * hjorne)) * 200, 300 + sin(radians(vinkel * hjorne)) * 200); } endShape(CLOSE); }Her har vi noen nye utregninger inne i kallet på
vertex. Her bruker vi tre nye funksjonercosogsinsom har blitt forklart lenger opp, ogradianssom regner grader om til radianer, en annen måleenhet for vinkler.I dataprogrammer bruker sinus og cosinus vanligvis radianer, så om vi vil jobbe med vinkler i grader, må vi gjør denne konverteringen. Du ser at vi har med en variabel for vinkelen mellom hvert punkt og denne har vi beregnet i grader ut fra at en sirkel er 360°.
Til slutt forteller
CLOSEiendShapeat siste kant i figuren skal settes sammen med første kant, altså at figures lukkes og fylles.
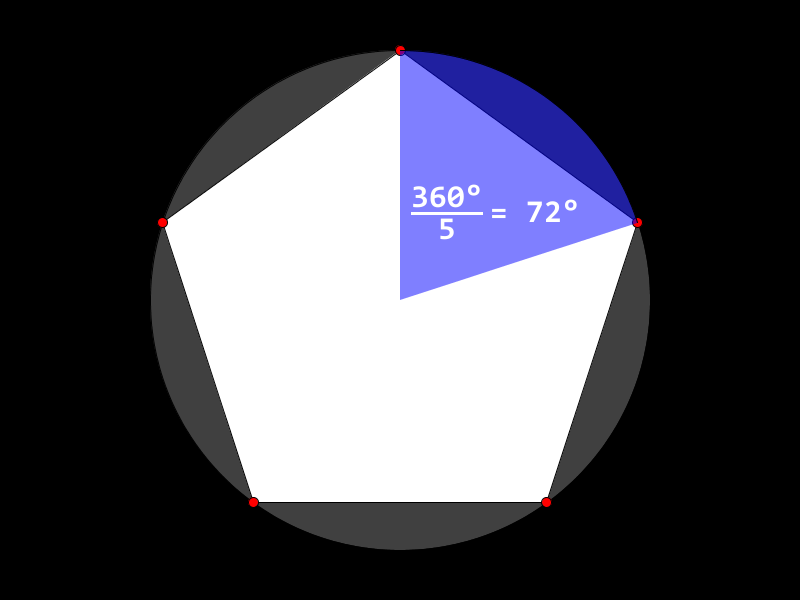
-
Hva er tallet
200her? Hva skjer om du endrer det til noe annet? -
Hva med tallet
300? -
Kan du få snudd på femkanten sånn at hjørnet som nå peker rett til høyre, peker opp?
- Hvis du har fått femkanten til å peke opp, kan du legge til en variabel som du bruker til denne justeringen? Kan du bruke denne variabelen til å få femkanten til å snurre?

-
Kan du styre hvilken vei femkanten peker med musa eller tastaturet?
-
Hva skjer hvis du endrer
KANTERtil en annen verdi enn5?
Regulære stjerner 1
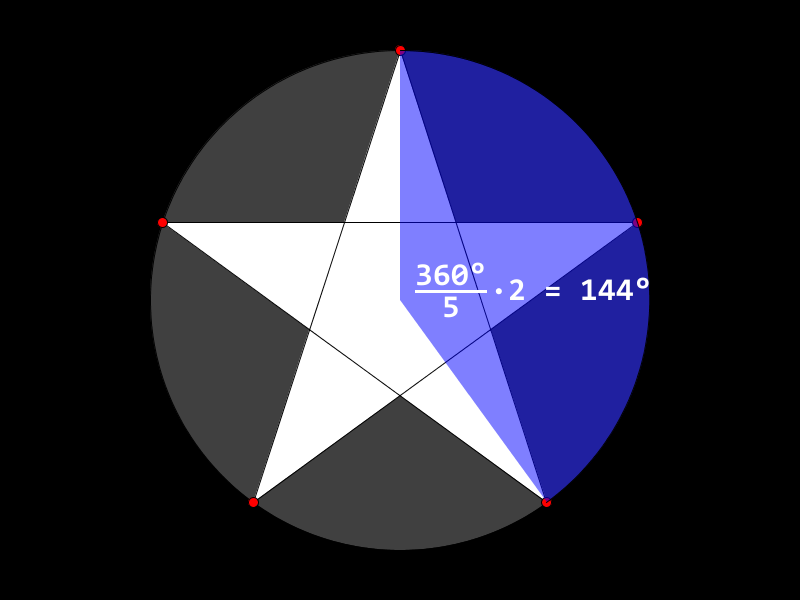
Regulære stjerner med et odde antall spisser kan tegnes nesten helt likt som man tegner en regulær mangekant. De kan nesten sees på som en variant av mangekanter. Hvis du har tegnet en femkantet stjerne før, har du kanskje lagt merke til at dette likner på en femkant, men at du hopper over et hjørne når du tegner streken mellom to spisser.
-
Siden vi skal hoppe over et hjørne hver gang vi tegner opp neste spiss, trenger vi å gange vinkelen med
2. Endre derfor kallet påvertextil:vertex(300 + cos(radians(vinkel * hjorne * 2)) * 200, 300 + sin(radians(vinkel * hjorne * 2)) * 200);Kunne du ganget med
2et annet sted i koden og fått den samme effekten? -
Kan du tegne en syvkantet stjerne? Eller en nikantet stjerne?
-
Hvis du har en stjerne med flere kanter enn fem, kan du gange med andre tall enn to og få andre varianter av mangekantede stjerner. Prøv forskjellige tall for syv-, ni- og ellevekantede stjerner. Hva skjer når du hopper over flere kanter enn halvparten av antallet spisser?
Regulære stjerner 2
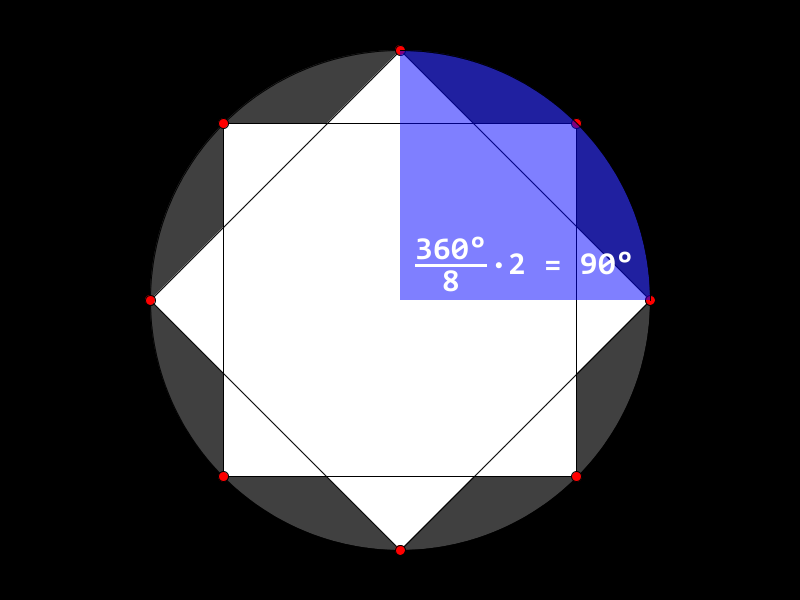
Stjerner med et likt antall spisser, kan tegnes som to regulære mangekanter med halvparten så mange hjørner som stjernen har spisser.
-
Fjern ganging med to om du nå tegner opp stjerner med odde antall spisser.
-
Lag en kopi av løkken som tegner opp mangekanten, med
beginShape();ogendShape(CLOSE);. -
I den nye løkken, endrer du
int hjorne = 0tilint hjorne = 1, slik at denne løkken tegner kantene mellom de odde hjørnene. -
Endre
hjorne++tilhjorne += 2sånn at vi bare tegner kanter mellom annenhvert hjørne. -
Pass på at
KANTERsettes til et partall som er minst6.
Utfordring
-
Nå ser det nok ut som om det mangler noen streker i stjernen din. Kan du få tegnet opp de siste kantene ved å tegne opp den første av de to mangekantene på nytt og bruke
noFill(),noStroke()ogstroke(). -
Kan du tegne opp flere mangekanter eller stjerner på skjermen samtidig? For eksempel en femkantet, en syvkantet og en nikantet stjerne som vist under?
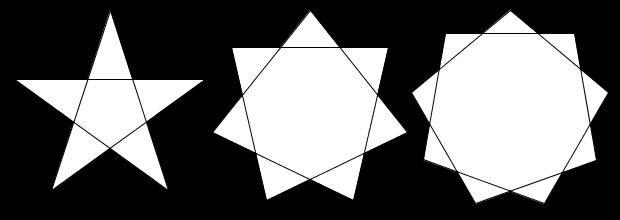
- Hvis stjernene dine ikke snurrer allerede, kan du få dem til å gjøre det?



